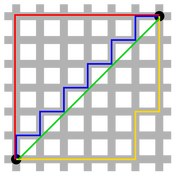
Taxicab Geometry was created by a man named Hermann Minkowski in 19th century in Germany. This type of geometry changes the Euclidean distance formula to the metric proposed by Hermann. He introduced the formula where distance between two points (x,y) and (w,z) is represented by the formula: d=|w-x| +|z-y|. The main idea behind the creation of this new distance formula was that the distance between those two points is not measured by a straight line but rather on a horizontal or vertical line as if traveling on an actual road. For example, in the picture provided above the red, blue, and yellow lines represent taxicab geometry.The parts that stay the same as in Euclidean geometry are the characteristics of points, lines, and angles.
Throughout the making of taxicab geometry there were a couple other people that were mentioned when researching about taxicab geometry. In 1952, Karl Menger created a geometry exhibit in Chicago named Museum of Science and Industry. Menger also wrote a booklet that was the first to mention the word taxicab geometry in it. By 1975, the taxicab geometry was still not talked about. Until, a man by the name Eugene Krause published a book called “Taxicab Geometry: An Adventure in Non-Euclidean Geometry. Once the book was published taxicab geometry people started to use it.
There are everyday uses that taxicab geometry relates too. For example, you can use taxicab geometry in chess. The distance between squares on the chessboard for rooks and bishops is measured in taxicab distance.
I think about how I could use this in a classroom. I feel this type of geometry could be for all ages. For instance, for younger grades you could create a map and in order to get to the next “hint” you need to figure out a path and how many steps you need to take. For the older grades, you could have them plot points on a graph and then figure out the distance between those points by counting the squares.
I really enjoy how flexible this geometry is in relation to how a teacher can use it. I’m glad I came to class and learned about this geometry because it could be a segway into other concepts in math a student may face.
Work cited:
http://taxicabgeometry.altervista.org/general/index.html
***picture from googling taxicab geometry
 RSS Feed
RSS Feed
