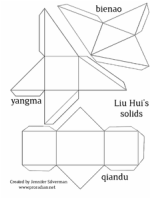
The most important aspect in this diagram is the relationship these three figures have with each other. She has stated that Bienao is one-sixth of the cube, Yangma is one-third of the cube, and Giandu is one-half of the cube. However, that is not all the relationship aspect she has created. She also states that the Bienao is one-third of the Giandu and one-half of the Yangma, and the Yangma is two-thirds of Giandu. Thus, you put them together to create a perfect cube.
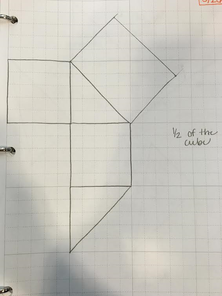
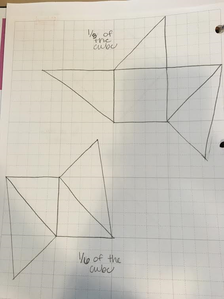
I think this topic of finding hidden shapes within shapes is so interesting; especially Jen’s thought process behind this creation. We got a chance to look at the cube that she created and tried to draw an outline in order to make the certain cubes. I thought doing this activity backwords (seeing the figure and then creating its shape) was interesting and challenging. My final work at the end of this blog.
I realized that in order to create the outline I needed to figure out common shapes that the three cubes shared. I found that each section either has a square or a triangle that is connected to another shape. After that I eye balled the image in which a certain shape is connected to that shared shaped. Overall, it was a guess and check mentality throughout finding these images. I thought it was also interesting that my drawing were different then her's but still made a cube in the end. Thus, it opens up the discussion with students about multiple approaches to figure out a problem. I would love to figure out multiple ways to approach this. I love that Jen approached it in a sense of finding a formula. Thus, making connections between geometry and algebra in an interactive way. If anyone can find her work or method I'd be interested in reading it. I've tried searching for it online but was running up short everytime.
If I were to incorporate this activity into a classroom, depending on the grade level, I would work backwards with the older children. With the younger elementary levels, I would see if from the diagram they can find common shapes and how these shapes are connected. Overall, I really liked how there were multiple relationship connections throughout this activity. I am very biased because I find it more entertaining to have hands on activities for students to learn by doing. Therefore, this activity fits my mentality down to a tee!
 RSS Feed
RSS Feed
